The Nature of Motion
Introduction
This lesson introduces the basics of motion and the application of simple physical principles and basic vector math to problems involving moving bodies. It culminates with an introduction to projectile motion and a presentation of Newton’s laws of motion, which summarize the classical view of physics.
Nature of Motion
The space that people perceive is filled with objects of various sizes and shapes, but these objects are not always in the same places. They change their distances and orientations relative to observers and to one another, although these changes do not take place all at once. Such changes are called motion, and they are measured as differences in position or orientation over time.
Systematically measuring motion requires standards of distance and time—two concepts that people use and understand in everyday situations but may have difficulty defining independently. Instead of tackling the philosophical problem of what time and distance are, most people take the pragmatic approach to using these concepts by employing a generally agreed-upon standard. For example, in the metric (SI) system, the meter (m) is the fundamental unit of length. Comparing the relative locations of objects to that standard enables an observer to measure the distance between them and report it in a way that others can understand.
Time is more esoteric. A standard for time requires reference to some periodic event (a concept that is itself based on some understanding of time). For example, the revolution of Earth around the sun (a year), the full rotation of Earth on its axis (a day), or even something as mundane as the drip of a faucet (a duration that depends on numerous factors) are periodic events that can be used as standards for time. In the metric (SI) system, the fundamental unit of time is the second (s). The critical point is that the event be periodic. Because it occurs at unchanging intervals, it provides a common standard of time to which everyone can refer.
Did You Know?

Time and distance are concepts that you use every day, but they are difficult to define because they are fundamental to human experience. Try thinking about how you would explain time or distance without referring to time or distance.

Vectors and Scalars
Determining the change in the distance or orientation of an object with respect to some standard of time yields a measurement of the object’s motion. Motion has two general characteristics: its direction and its quickness. Therefore, vectors are helpful in quantifying motion. A vector is a quantity that has a direction and a length (or magnitude) but no defined location. It is often depicted as an arrow that begins at one point (called the tail) and ends at another point (called the head). Because a vector has no location, it can move anywhere and remain the same vector. Variables representing vectors often appear in boldface (e.g., v) or with a small arrow above them (e.g., \(vec{v}\)).
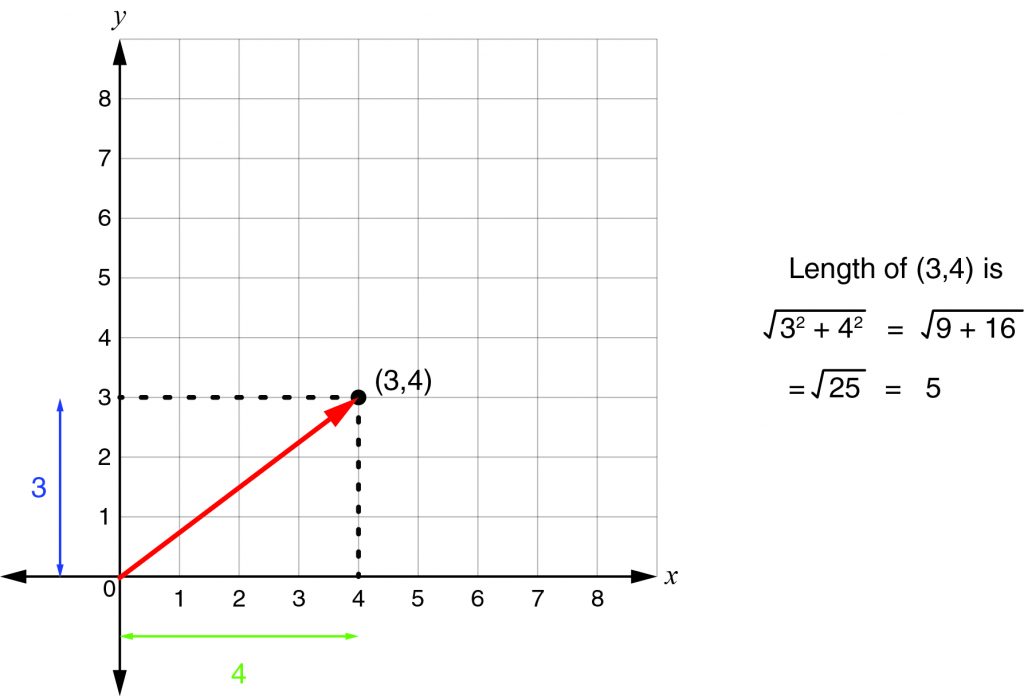
In a rectangular coordinate system, one representation of a vector is the coordinates of the head when the tail is at the origin. For example, a vector in two dimensions might be expressed as (3, –5). Because vectors have no location, however, the same vector can have its tail elsewhere. To return it to the origin, subtract the coordinates of the tail from the respective coordinates of the head to yield the standard vector form. To find the length of a vector expressed in standard form, square each of the coordinates, add them, and take the square root of the sum. This process is an application of the Pythagorean theorem for right triangles.
In contrast with a vector is a scalar, which has a magnitude but no direction. A simple number such as 5 or 10.2 is a scalar. The length of a vector, for example, is a scalar.
Basic Vector Operations
Adding two or more vectors yields a resultant. Graphically, adding two vectors involves placing the tail of one on the head of the other (and continuing this process when adding more vectors). The resultant is a new vector starting at the tail of the first and ending at the head of the second. Because the resultant vector is the same regardless of which way the vectors are added, vector addition is commutative (meaning \(vec{a} + vec{b} = vec{b} + vec{a}\)). Adding vectors in coordinate form just requires adding the respective coordinates of each.
For example, (7, 1) + (2, –3) = (7 + 2, 1 + [–3]) = (9, –2).
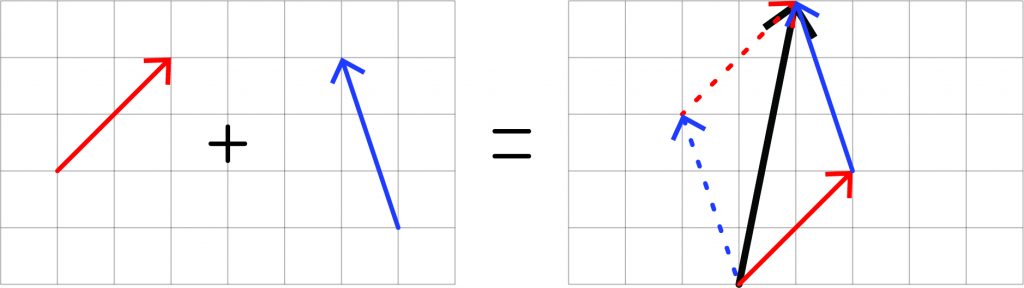
Subtracting vectors follows similar rules: for example, (7, 1) – (2, –3) = (7 – 2, 1 – [–3]) = (5, 4).
Key Point

Remember that because vectors have no location, they can be moved as necessary to aid in visualization, addition, or any number of purposes. As long as two vectors have the same direction and length (magnitude), they are the same vector.
To multiply a vector by a scalar, multiply each coordinate in the vector by that scalar. To divide a vector by a scalar, divide each coordinate by that scalar. Dividing a vector by its length (or, equivalently, multiplying by the reciprocal of its length) yields a new vector that has the same direction as the original but a length 1. Such a vector is called a unit vector. These rules also allow vector subtraction to be expressed as vector addition: \(vec{a} –vec{b} = vec{a} + (–1 × vec{b}) = vec{a} + (–vec{b})\). They also enable easier graphical addition of vectors.
Velocity and Acceleration
Because motion has a direction and a magnitude of some type, vectors are a way to quantify it. One measurement of how quickly an object is moving is speed: the distance from one point to another divided by the travel time. For instance, if a plane moves 252 meters in 2.00 seconds, its speed is 252 meters ÷ 2.00 seconds = 126 meters per second (m/s). But for passengers on that plane, the direction of flight is just as important as the speed. Thus, multiplying the speed by a unit vector in the direction of travel yields a vector called velocity.
Key Point

The velocity of an object is a vector: it quantifies both the magnitude and the direction of the object’s motion. The speed of an object is a scalar: it is just the magnitude of its motion. Therefore, two objects can have the same speed but different velocities.
The rate at which velocity changes is called acceleration. Like velocity, acceleration has a magnitude and a direction, so it can be expressed as a vector. (Note that the term acceleration can also mean the magnitude of the acceleration vector, which is a scalar. The context of the problem will generally clarify whether the term refers to a vector or a scalar.) For instance, if a truck moving in a straight line is speeding up, its acceleration is in the same direction as its velocity; if the truck is slowing down, its acceleration is in the direction opposite to its velocity.
Quantitatively, the magnitude of the acceleration is the difference in speed divided by the elapsed time.
Keep In Mind

These simple mathematical definitions of velocity and acceleration assume constant speed and acceleration scalars, respectively, over the time period in the calculation. If the speed or acceleration is changing, they yield average values for that time period.
Projectile Motion
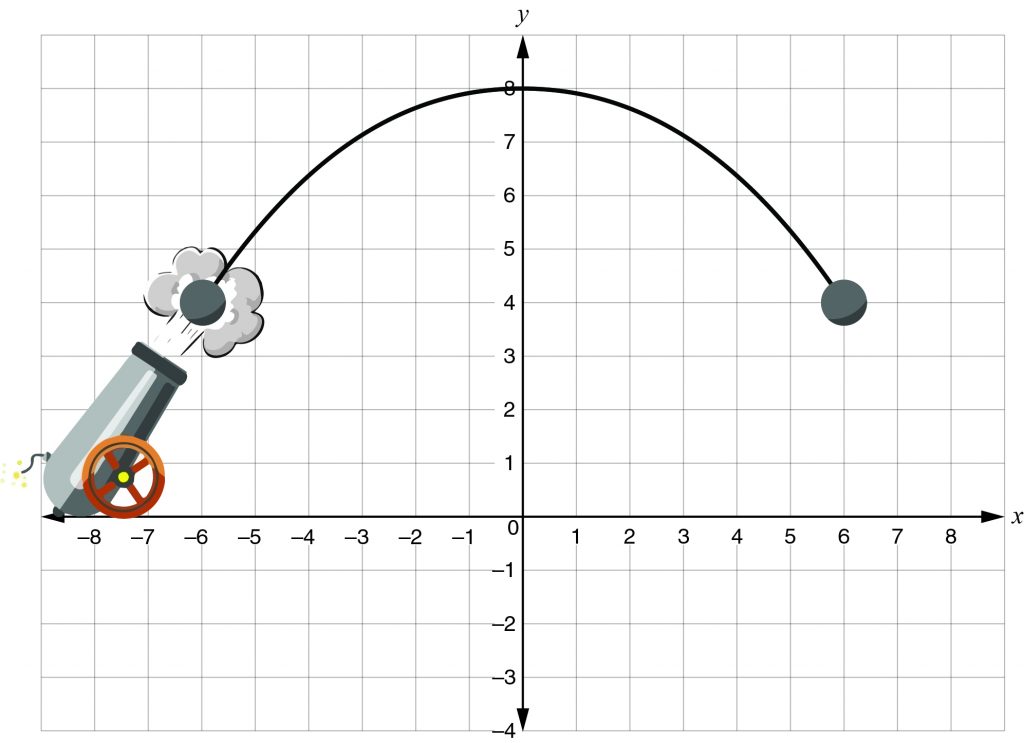
One special case of motion involves an object moving under the influence of gravity—for example, when a player hits a baseball or a cannon fires a cannonball. Ignoring any other forces (including air resistance), such an object moves in two dimensions, generally combining a horizontal component of motion and a vertical component. It experiences downward acceleration of 9.8 meters per square second \((m/s^2)\) but no horizontal acceleration.
Given a horizontal speed \(v_x\) and an initial horizontal position (coordinate) \(x_i\), the object’s horizontal position (assuming a starting time of t = 0) is \(x(t)=x_i + v_xt\). However, the object’s vertical distance from its starting point is complicated by the acceleration due to gravity. Some basic calculus shows that given an initial vertical speed \(v_y\) and an initial vertical position (coordinate) \(y_i\), the object’s vertical position (assuming a starting time of t = 0) is:
\(y(t)=–frac{1}{2}gt^2 + v_yt + y_i\)
Note that g is the acceleration due to gravity \((9.8 m/s^2)\) and that the quadratic term is negative because gravity accelerates an object downward. Plotting the coordinates of the object at various times shows that it traces a parabola.
Be Careful

Make sure you know the height of the ground when analyzing projectile motion. Generally, an object won’t be able to go any lower than ground level!
Newton’s Laws of Motion
Newton’s laws of motion summarize the qualitative characteristics of moving objects. These laws refer to two important concepts in physics: force and mass. A force is a “push” or “pull” that an object experiences or exerts on another object; it is also a vector with a direction and magnitude. Mass is in some sense resistance to movement (or “displacement”) by a force; it is a scalar. Thus, given a certain force, an object with less mass will move more than an object with more mass.
- Newton’s first law of motion, which deals with inertia, states that an object in motion will remain in motion unless a net force acts on it and that an object at rest will remain at rest unless a net force acts on it. Note that net force just means the object feels some force: it is the resultant of all forces acting on the object. If two people push with the same force against a cart but direct their efforts in precisely opposite directions, the cart will feel no net force. Another way to understand this law is that an object’s velocity will stay the same unless a force acts on the object.
- Newton’s second law of motion relates an object’s mass, its acceleration, and the (net) force acting on it. This law says the force on an object (a vector \(vec{F}\)) produces acceleration of the object (\(vec{a}\)) that is proportional to the object’s mass (m). Hence the well-known equation \(vec{F} = mvec{a}\) (or F = ma when dealing only in magnitudes—that is, scalars—not directions.) In SI units, the force is in newtons (N), the mass is in kilograms (kg), and the acceleration is in meters per square second \((m/s^2)\). Qualitatively, this law says that accelerating more-massive objects requires a greater force than accelerating less-massive objects.
- Newton’s third law of motion states that when an object exerts a force on another object, it experiences a force of equal magnitude but opposite direction from that other object. This law is sometimes expressed by saying that for every action, there is an equal and opposite reaction.
Let’s Review
- Motion is the change in an object’s position or orientation over time.
- Measurement of motion requires a consistent, accessible standard of distance and time.
- A vector is a quantity with magnitude and direction but no location; a scalar has a magnitude but no direction.
- The standard notation form of a vector is the coordinates of its head when its tail is at the origin of the coordinate system. If the vector is shown elsewhere, subtract the coordinates of the tail from the respective coordinates of the head to get the standard form.
- To multiply a scalar and a vector, multiply each coordinate of the vector by the scalar: a × (x,y) = (ax,ay).
- To calculate the resultant, or sum, of two vectors, add the respective coordinates of those vectors: (a, b) + (c, d) = (a + c, b + d).
- To find the length of a vector, square its coordinates, add them, and take the square root.
- Vector addition is commutative: \(vec{a} + vec{b} = vec{b} + vec{a}\).
- Velocity is a vector that represents how quickly an object is moving. Speed is the magnitude of that vector (it is a scalar).
- Acceleration is a vector that represents how quickly the velocity is changing.
- Projectile motion is the motion of an object under the influence of gravity. Such an object follows a parabolic path. Its horizontal position at time t, given initial horizontal velocity \(v_x\) and initial horizontal position \(x_i\), is \(x(t) = x_i + v_x × t\). Its vertical position at time t, given initial vertical velocity \(v_y\) and initial vertical position \(y_i\), is \(y(t) = –frac{1}{2}gt^2 + v_yt + y_i\).
- Newton’s laws of motion summarize motion in classical physics.
- Newton’s first law is that an object at rest stays at rest and an object in motion stays in motion, unless a net force acts on the object.
- Newton’s second law is that the net force, object mass, and acceleration are related by \(F = m×vec{a}\) (or F = m × a when dealing only in magnitudes).
- Newton’s third law is that an object exerting a force on another object feels the same force, but in the opposite direction.
Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
