Kinetic Energy
This lesson introduces the concept of mechanical energy as the sum of kinetic energy and potential energy. The lesson also examines objects in motion and the effects of changing velocities and forces on moving objects. Finally, the lesson discusses how the force of gravitation affects objects in the universe.
Mechanical Energy
Energy is the ability to do work. Mechanical energy can be divided into two types: kinetic energy and potential energy.
Kinetic energy of an object is represented by the equation \(KE=\frac{1}{2}mv^2\), where m is the mass of the object and v is the velocity. The kinetic energy is proportional to the object’s mass. A 7.26 kg shot thrown through the air has much more kinetic energy than a 145 g baseball with the same velocity. The kinetic energy of an object is also proportional to the square of the velocity of the object. A car traveling at 40 m/s has four times the kinetic energy of the same car moving at 20 m/s. This is the result of the squared velocity term in the formula. Kinetic energy, like work, is measured in joules.
Consider a group of boulders perched high on a cliff. These boulders have energy in a stored condition because gravity could cause them to fall. This is called gravitational potential energy (there are other types of stored energy, such as chemical and electrical). Potential energy of an object is stored energy due to the object’s configuration or position relative to a force acting on it. The formula for calculating gravitational potential energy is PE = mgh, where m is the mass of the object, g is the acceleration of gravity on Earth \((9.8 m/s^2)\), and h is the object’s height above Earth’s surface. The unit for potential energy is also joules. Potential energy is an energy of position because much of the way this quantity can be changed is due to height.
Falling objects provide an interesting case for mechanical energy calculations. If we assume that there is no wind resistance, then all potential energy an object has before falling turns into kinetic energy as the object falls. Once the object impacts Earth’s surface, there are different calculations to be done. We will simplify things by considering the object at the moment before impact.
Linear Momentum and Impulse
The momentum of an object depends upon its mass and velocity. Momentum is defined as p = mv, where m is the mass and v is the velocity. The unit for momentum is kg·m/s and does not have a special name. This concept can be illustrated by a simple example: Most people would rather try stopping a child’s tricycle rolling at 0.5 miles per hour than a loaded dump truck at the same speed. The difference is the dump truck’s greater momentum as a result of its much larger mass.
Newton’s second law of motion explains how the momentum of an object is changed by a net force acting upon it. Newton’s second law of motion, F = ma, can be rewritten by using the definition of acceleration as the change in velocity divided by the time interval.
\(F = ma = m(frac{Delta v}{Delta t})\)
Multiplying both sides of the equation by the time interval results in the following equation:
\(FΔt = mΔv\)
The left side, FΔt, is the product of the average force and the time interval over which it acts. This product is called the impulse, and an impulse is found by determining the area under the curve of a force-time graph, as shown below.
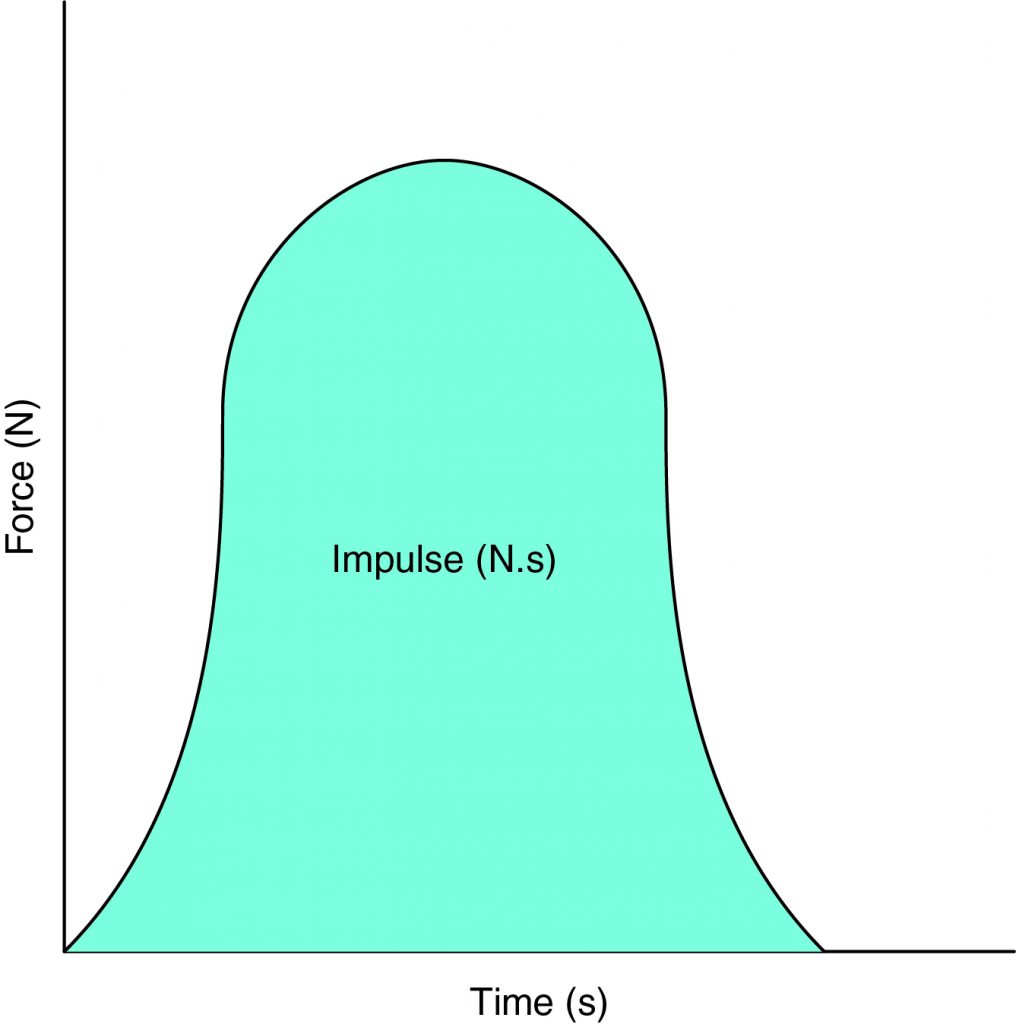
Impulse-Momentum Theorem: \(FΔt = p_2 − p_1\)
This equation is called the impulse-momentum theorem. The impulse on an object is equal to the change in momentum that it causes. If the force is constant, the impulse is just the product of the force and the time interval over which it acts.
What happens to a driver when a crash suddenly stops a car? An impulse is needed to bring the driver’s momentum to zero. The steering wheel can exert a large force during a short period of time. An airbag reduces the force exerted on the driver by greatly increasing the length of the time over which the force is exerted.
Refer to the equation: F = (mΔv)/Δt. In the equation, Δv is the same with or without the airbag. However, the airbag reduces F by increasing Δt. Less force on a person during a crash is a good thing.
Universal Gravitation
Newton used mathematical arguments to show that if the path of a planet is an ellipse, then the magnitude of the force, F, on the planet resulting from the sun must vary inversely with the square of the distance between the center of the planet and center of the sun.
Newton later stated that the sight of a falling apple made him think about the motion of planets. He recognized that the apple fell straight down because Earth attracted it. He wondered whether this force might extend beyond the trees to the clouds, to the moon, and beyond. Could gravity also be the force that attracts the planets to the sun? Newton hypothesized that the force on the apple must be proportional to its mass. In addition, according to Newton’s third law of motion, the apple would also attract Earth. Thus, the force of attraction must be proportional to the mass of Earth. The attractive force that exists between all objects is known as gravitational force.
Newton assumed that the same force of attraction would act between any two masses, \(m_1\) and \(m_2\). He proposed his law of universal gravitation, which is represented by the following equation:
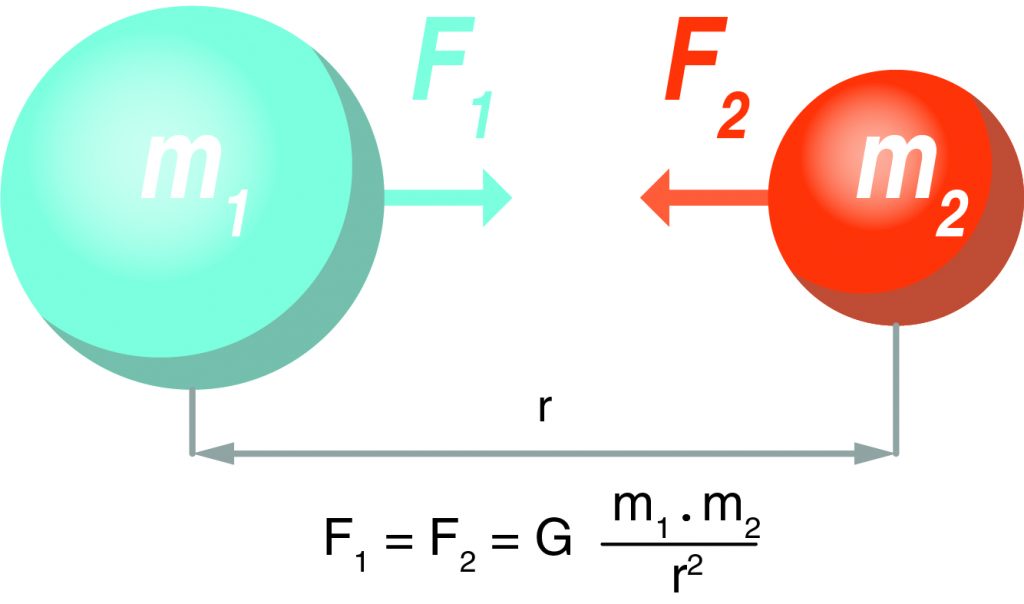
In the equation, r is the distance between the centers of the masses, and G is a universal constant—that is, it is the same everywhere. The gravitational constant \(G = 6.67 × 10-11 N∙m^2/kg^2\). The force of gravitation is directly proportional to the masses of the objects. However, force is inversely proportional to the square of the distance between the objects.
Let’s Review!
- Kinetic energy, or the energy of motion, of an object is represented by the equation \(KE=\frac{1}{2}mv^2\).
- The potential energy of an object is stored energy due to the object’s configuration or position relative to a force acting on it. Gravitational potential energy is defined as PE = mgh. Near Earth’s surface, gravitational acceleration is measured to be \(g = 9.8 m/s^2\).
- Newton’s second law of motion explains how the momentum of an object is changed by a net force action on it.
- The impulse on an object is equal to the change in momentum that it causes.
- The attractive force that exists between all objects is known as the gravitational force. That force is directly related to the product of the two masses and inversely related to the square of the distance between the masses.
- \(F=G(frac{m_1 m_2}{r^2})\) where \(G= 6.67times 10^{-11} \frac{N.m^2}{kg^2}\)
Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
