Measurement and Dimension
This lesson applies the formulas of volume for cylinders, pyramids, cones, and spheres to solve problems.
Volume of a Cylinder, Cone, and Sphere Review
Volume of a Cylinder
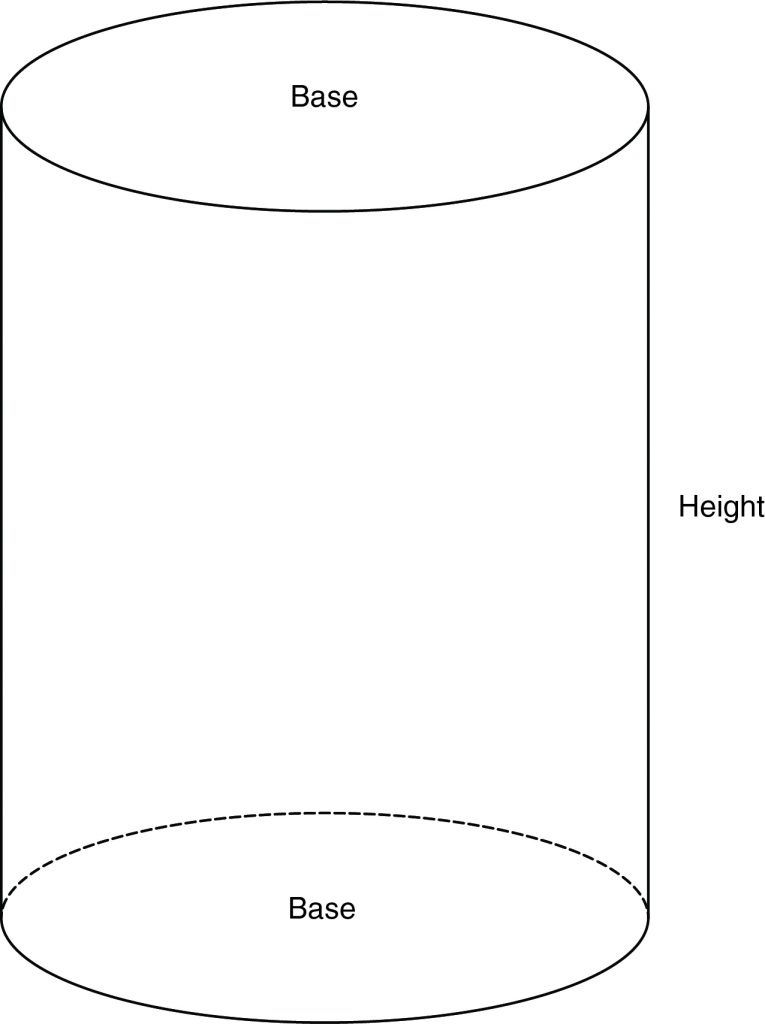
A cylinder is a three-dimensional figure with two identical circular bases and a rectangular lateral face.

KEEP IN MIND
The volume of a cylinder can be expressed in terms of π, and the volume is measured in cubic units.
The volume of a cylinder equals the product of the area of the base and the height of the cylinder. This is the same formula used to calculate the volume of a right prism. In this case, the area of a base is a circle, so the formula is \( V = Bh = πr^2 h\). The height is the perpendicular distance between the two circular bases.
Example
Volume of a Pyramid and a Cone
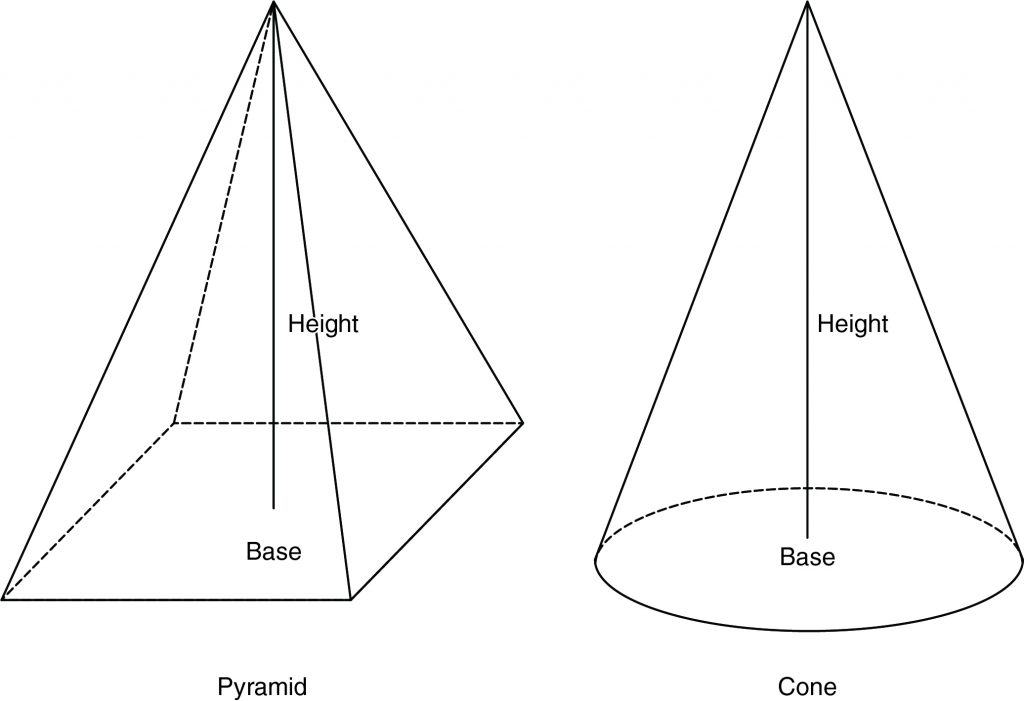
A pyramid is a three-dimensional solid with one base and all edges from the base meeting at the top, or apex. Pyramids can have any two-dimensional shape as the base. A cone is similar to a pyramid, but it has a circle instead of a polygon for the base.

BE CAREFUL!
Make sure that you apply the correct formula for area of the base for a pyramid.
The formula for the volume of a pyramid is similar to a prism, \(V = \frac{1}{3} Bh\) where B is the area of the base; in the case of a hexagonal pyramid B is = to \(\frac{1}{2}\) (apothem)(perimeter). The base is a circle for a cone, and the formula for the volume is \(V = \frac{1}{3} Bh = \frac{1}{3} π r^2 h\).
Examples
Volume of a Sphere
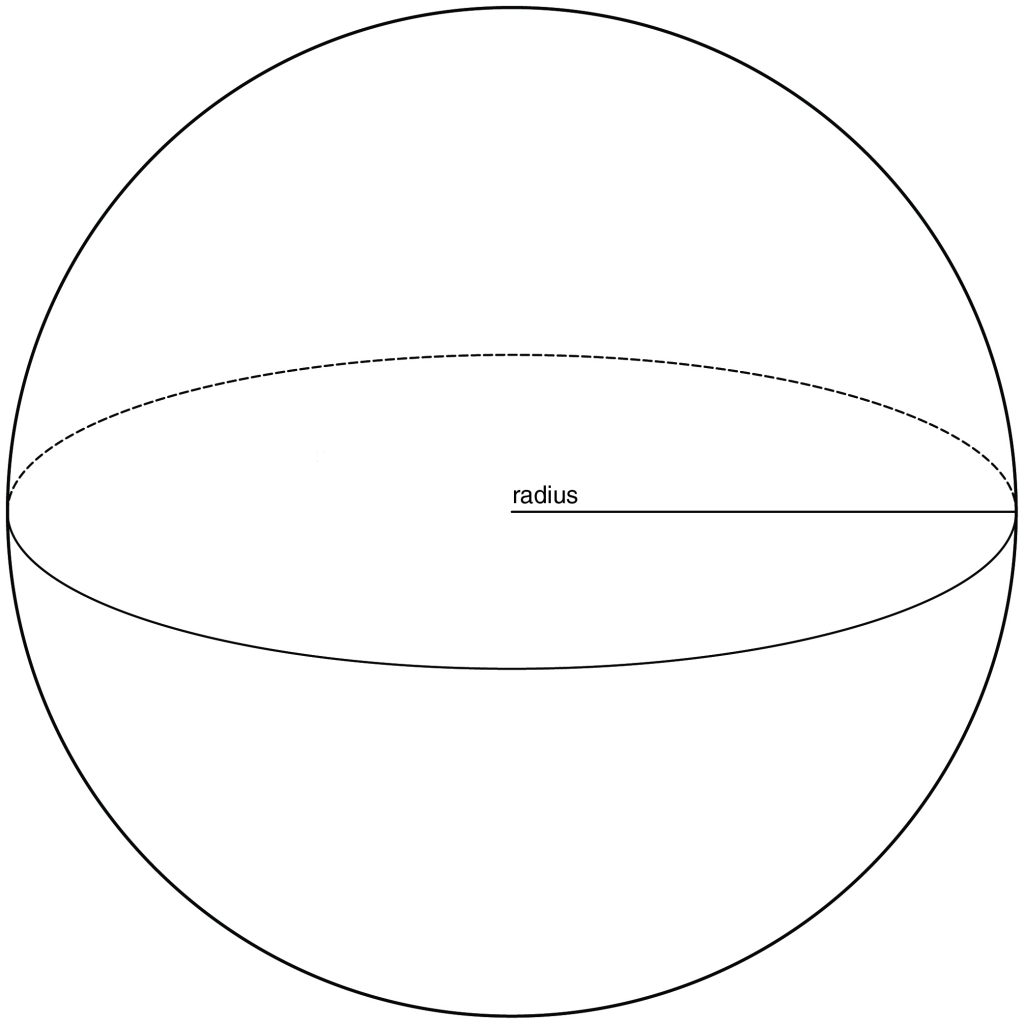
A sphere is a round, three-dimensional solid, with every point on its surface equidistant to the center. The formula for the volume of a sphere is represented by just the radius of the sphere. The volume of a sphere is \(V = \frac{4}{3} π r^3\). The volume of a hemi (half) of a sphere is \(V = (\frac{1}{2}) \frac{4}{3} π r^3 = \frac{2}{3} π r^3\).

BE CAREFUL!
The radius is cubed, not squared, for the volume of a sphere.
Example
Let’s Review!
- The volume is the capacity of a three-dimensional object and is expressed in cubic units.
- The volume formula for a cylinder is the product of the area of the base (which is a circle) and the height of the cylinder.
- The volume formula for a pyramid or cone is one-third of the product of the area of the base (a circle in the case of the cone) and the height of the pyramid or cone.
- The volume formula for a sphere is \(V = \frac{4}{3} π r^3\).
Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
