Introduction to Physics

Newton’s Laws of Motion

• Newton’s laws of motion summarize motion in classical physics.
• Newton’s first law is that an object at rest stays at rest and an object in motion stays in motion, unless a net force acts on the object.
• Newton’s second law is that the net force \((vec{F})\), object mass (m), and acceleration \((vec{a})\) are related by \(F = m×vec{a}\) (or F = m × a when dealing only in magnitudes).
• Newton’s third law is that an object exerting a force on another object feels the same force, but in the opposite direction.

Friction

• Linear motion is movement along a line; the velocity and acceleration may vary, but they are always parallel to the line.
• Nonlinear motion is movement that is not confined to a line; the velocity and acceleration can be any quantity.
• Rotational (circular) motion is movement around an axis or along a circular path.
• The period (T) of an object in uniform circular motion is the time it takes to travel once around the circle. Given a radius r  and a time T  to go around the circle, the speed v  is \(V = frac{2πr}{T}\) .
• The inverse of the period is the frequency (f), and the angular frequency (ω) is 2πf which may use hertz. The velocity is ωr = 2πfr.
• Centripetal acceleration \((a_c)\) is the acceleration an object experiences when in uniform circular motion. It can be represented as \(a_c = frac{v^2}{r}\) , where v  is the object’s velocity and r  is the radius of the circle of motion.
• The centripetal force on an object in uniform circular motion is the object’s mass times its centripetal acceleration. It can be represented as \(F_c\) = \(ma_c\) =  \(\frac{mv^2}{r}\).
• Centrifugal force is a “ghost force” in which an object undergoing centripetal acceleration “feels” like it is being pushed away from the center of rotation.
• Friction is resistance to motion. It is a force that is generally directed opposite  to a moving object’s velocity.
• Friction causes heat and/or motion of surrounding materials as a byproduct of its force on a moving object.
• Friction can prevent motion by acting opposite to other forces, such as gravity.

Waves and Sound

• Waves occur throughout nature in different forms, but they have common properties and behaviors.
• A wave is defined by its amplitude, frequency, and wavelength. The wave speed is equal to the product of the wavelength and frequency which is often expressed in Hz  hertz (v = λf).

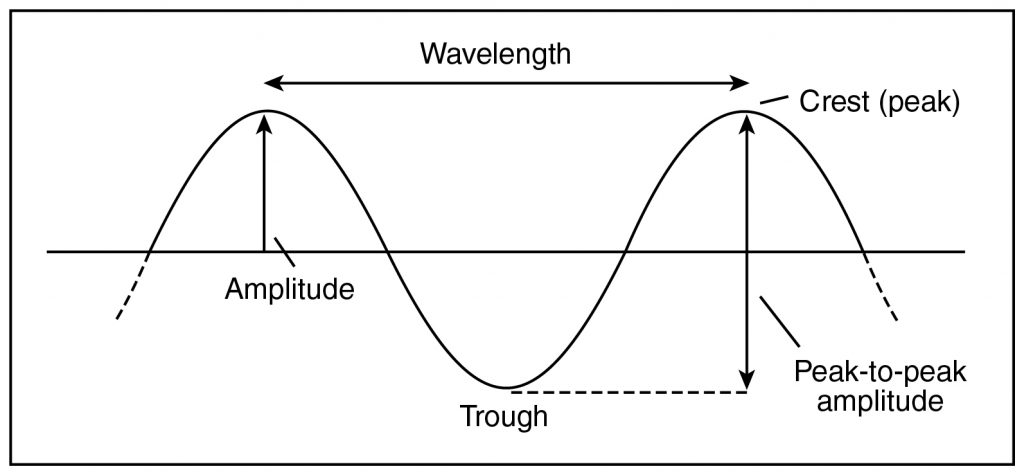
• Common wave behaviors include reflection (when the wave “bounces” off an object), refraction (when it bends in a medium), and diffraction (when it turns around an edge).
• Mechanical waves are waves in a material—solid, liquid, or gas. Examples include sound waves, seismic waves, and ocean waves. In the case of sound, ear detects pitch which is essentially the frequency of the wave, and the volume is essentially the amplitude.
• The speed of a mechanical wave depends on the compressibility and density of a material. As these values increase, so does the wave speed.
• Electromagnetic waves are a back-and-forth oscillation of the electric and magnetic fields owing to acceleration of a charge. They can propagate without a medium (that is, in a vacuum).
• The speed of an electromagnetic wave in a material is equal to the speed of light in a vacuum (c) divided by the refractive index of that material.
• Rays are directed line segments that represent the waves that may be much larger than the wavelength of the electromagnetic waves/dimensions of a problem.
• In optics, the angle of incidence of a light ray (like with a mirror) is equal to the angle of reflection.
• Refraction of a ray is described by Snell’s law: \(\frac{sin theta_i}{sin theta_r}=\frac{n_r}{n_i}\), where \(θ_i\) is the angle of incidence, \(θ_r\) is the angle of refraction, \(n_i\) is the refractive index in the material from which the ray is traveling, and \(n_r\) is the refractive index in the material to which the ray is traveling.

Kinetic Energy

• Kinetic energy, or the energy of motion, of an object is represented by the equation KE = mv2, where m is the mass of the object and v is the velocity.
• The potential energy of an object is stored  energy due to the object’s configuration or position relative to a force acting on it. Gravitational potential energy is defined as PE = mgh, where m  is the mass of an object and h  is the object’s height. Near Earth’s surface, gravitational acceleration is measured to be g = 9.8 m/s2. The unit for potential energy is joules.
• Momentum is defined as p = mv, where m  is the mass and v  is the velocity. The unit for momentum is kg·m/s and does not have a special name.
• Recall that Newton’s second law of motion explains how the momentum of an object is changed by a net force action on it.
• Newton’s second law of motion, F = ma, can be rewritten by using the definition of acceleration as the change in velocity divided by the time interval. \(F = ma = m(frac{Delta v}{Delta t})\) or FΔt = mΔv.
• The impulse on an object is equal to the change in momentum that it causes.
• The attractive force that exists between all objects is known as gravitational force. That force is directly related to the product of the two masses and inversely related to the square of the distance between the masses.
• Newton has an additional law: the law of universal gravitation where the force of gravitation (G) is directly proportional to the masses of the objects, and represented with a constant. \(F=G(frac{m_1 m_2}{r^2})\) where the constant \(G= 6.67times 10^{-11} \frac{N.m^2}{kg^2}\). 

Electricity and Magnetism

• Electric charges, which can be either positive or negative, create electric fields and exert an electric force on other charges.
• The electric force between two charges (\(Q_1\) and \(Q_2\)) obeys Coulomb’s law: \(F_E=kfrac{Q_1Q_2}{r^2}\) , where k  is the electric constant (about \(9 × 10^9\) when working in SI units) and r  is the distance between the charges.
• The electric field from a charge Q is \(E=kfrac{Q}{r^2}\).
• Magnetic fields and forces result from moving charges (an electric current). Magnets have north and south polarities, but unlike electricity where negative and positive charges can appear separately, these magnetic polarities always appear together.
• Electric flux is the “flow” of the electric field, which can be visualized using electric field lines.
• Magnetic flux is the “flow” of the magnetic field, which can be visualized using magnetic field lines.
• Changing magnetic flux through a surface creates an electric field through that surface—a phenomenon that enables electricity generation.
• An Electric circuit is a closed “loop” that involves current flowing through resistors and other electrical components, driven by an electric potential difference (voltage).
• Ohm’s law is represented as V = RI, the voltage across a resistor is equal to the product of the resistance and the current. Common units for these parameters are volts, ohms, and amperes.