Polynomials
This lesson introduces adding, subtracting, and multiplying polynomials. It also explains polynomial identities that describe numerical expressions.
Adding and Subtracting Polynomials
A polynomial is an expression that contains exponents, variables, constants, and operations. The exponents of the variables are only whole numbers, and there is no division by a variable. The operations are addition, subtraction, multiplication, and division. Constants are terms without a variable. A polynomial of one term is a monomial; a polynomial of two terms is a binomial; and a polynomial of three terms is a trinomial.

KEEP IN MIND
The solution is an expression, and a value is not calculated for the variable.
To add polynomials, combine like terms and write the solution from the term with the highest exponent to the term with the lowest exponent. To simplify, first rearrange and group like terms. Next, combine like terms.
![]()
To subtract polynomials, rewrite the second polynomial using an additive inverse. Change the minus sign to a plus sign, and change the sign of every term inside the parentheses. Then, add the polynomials.
![]()
![]()
Examples
Adding and Subtracting Polynomials Review
Multiplying Polynomials
Multiplying polynomials comes in many forms. When multiplying a monomial by a monomial, multiply the coefficients and apply the multiplication rule for the power of an exponent.
![]() .
.
BE CAREFUL!

Make sure that you apply the distributive property to all terms in the polynomials.
- When multiplying a monomial by a polynomial, multiply each term of the polynomial by the monomial.
![]()
- When multiplying a binomial by a binomial, apply the distributive property and combine like terms.
![]()
- When multiplying a binomial by a trinomial, apply the distributive property and combine like terms.
![]()
Examples
Multiplying Polynomials Review
Polynomial Identities

BE CAREFUL!
Pay attention to the details of each polynomial identity and apply them appropriately.
There are many polynomial identities that show relationships between expressions.
- Difference of two squares:
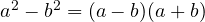
- Square of a binomial:
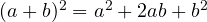
- Square of a binomial:
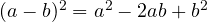
- Sum of cubes:
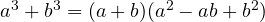
- Difference of two cubes:
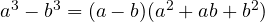
Examples
Polynomial Identities Review
Let’s Review!
- Adding, subtracting, and multiplying are commonly applied to polynomials. The key step in applying these operations is combining like terms.
- Polynomial identities require rewriting polynomials into different form
