Similarity, Right Triangles, and Trigonometry
This lesson defines and applies terminology associated with coordinate planes. It also demonstrates how to find the area of two-dimensional shapes and the surface area and volume of three-dimensional cubes and right prisms.
Coordinate Plane
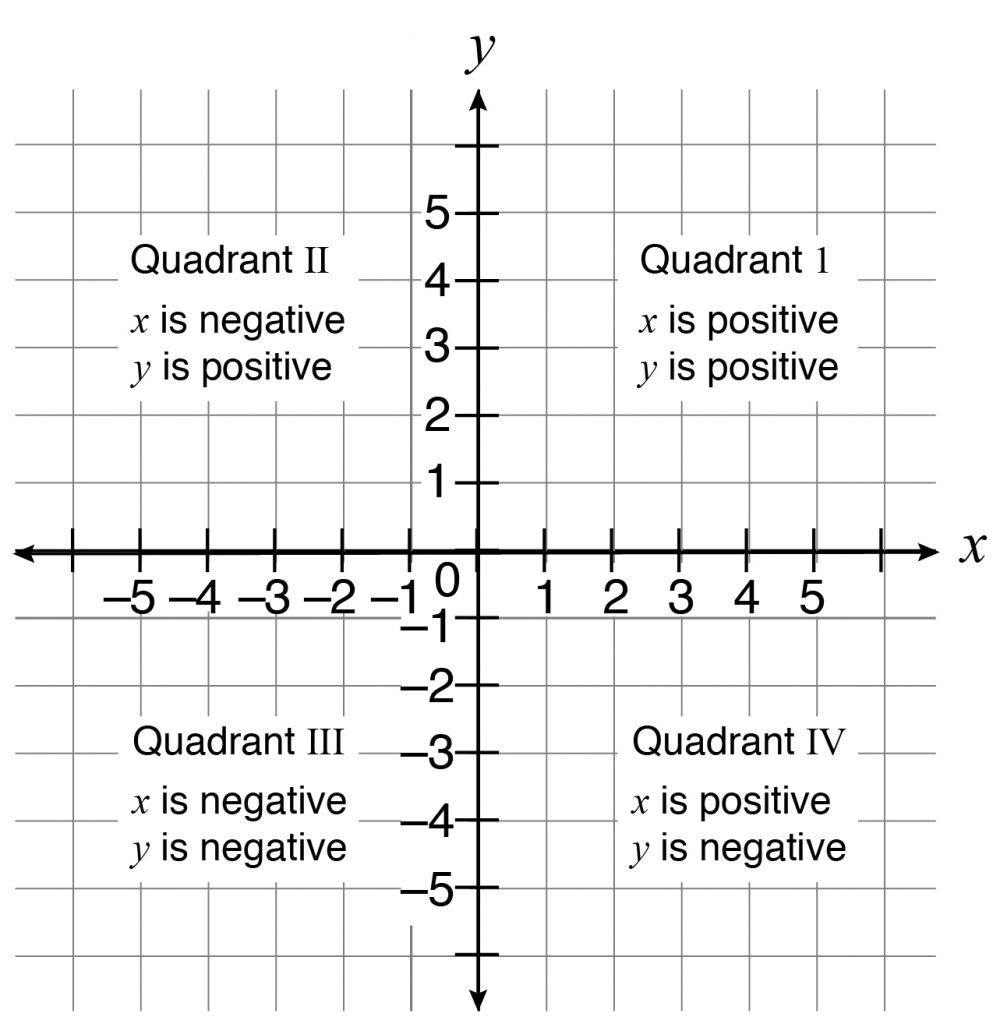
The coordinate plane is a two-dimensional number line with the horizontal axis called the x-axis and the vertical axis called the y-axis. Each ordered pair or coordinate is listed as (x, y). The center point is the origin and has an ordered pair of (0, 0). A coordinate plane has four quadrants.
Keep In Mind

The x-coordinates are positive to the right of the y-axis. The y-coordinates are positive above the x-axis.
To graph a point in the coordinate plane, start with the x-coordinate. This point states the number of steps to the left (negative) or to the right (positive) from the origin. Then, the y-coordinate states the number of steps up (positive) or down (negative) from the x-coordinate.
Given a set of ordered pairs, points can be drawn in the coordinate plane to create polygons. The length of a segment can be found if the segment has the same first coordinate or the same second coordinate.

PRO TEST TIP
While your test may not directly test you on graphing, understanding the coordinate plane is an essential skill in reading graphs and extending your knowledge to area and dimension for geometric figures. Graphs can be helpful for visualizing area, but the geometry section is largely meant to test for the ability to use equations properly.
Coordinate Plane Review
Area of Two-Dimensional Objects
The area is the number of unit squares that fit inside a two-dimensional object. A unit square is one unit long by one unit wide, which includes 1 foot by 1 foot and 1 meter by 1 meter. The unit of measurement for area is units squared (or feet squared, meters squared, and so on). The following are formulas for calculating the area of various shapes.
- Rectangle: The product of the length and the width, \(A = lw\).
- Parallelogram: The product of the base and the height, \(A = bh\).
- Square: The side length squared, \(A = s^2\).
- Triangle: The product of one-half the base and the height, \(A =\frac{1}{2}bh\).
- Trapezoid: The product of one-half the height and the sum of the bases, \(A =\frac{1}{2}h(b_1+b_2)\).
- Regular polygon: The product of one-half the apothem (a line from the center of the regular polygon that is perpendicular to a side) and the sum of the perimeter, \(A =\frac{1}{2}ap\).

Be Careful

Make sure that you apply the correct formula for area of each two-dimensional object.
Area of Two-Dimensional Objects Review
Surface Area and Volume of Cubes and Right Prisms
A three-dimensional object has length, width, and height. Cubes are made up of six congruent square faces. A right prism is made of three sets of congruent faces, with at least two sets of congruent rectangles.

Be Careful
Surface area is a two-dimensional calculation, and volume is a three- dimensional calculation.
The surface area of any three-dimensional object is the sum of the area of all faces. The formula for the surface area of a cube is \(SA = 6s^2\) because there are six congruent faces. For a right rectangular prism, the surface area formula is \(SA = 2lw + 2lh + 2hw\) because there are three sets of congruent rectangles. For a triangular prism, the surface area formula is twice the area of the base plus the area of the other three rectangles that make up the prism.
The volume of any three-dimensional object is the amount of space inside the object. The volume formula for a cube is \(V = s^3\). The volume formula for a rectangular prism is the area of the base times the height, or \(V = Bh\).
Surface Area and Volume of Cubes and Right Prisms Review
Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry discovered by the ancient Greek mathematician Pythagoras. It relates to the sides of a right triangle and states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In a right triangle with side lengths a, b, and hypotenuse c, the Pythagorean Theorem is represented by the equation: a² + b² = c²
where:
- c represents the length of the hypotenuse (the side opposite the right angle),
- a and b denote the lengths of the other two sides.
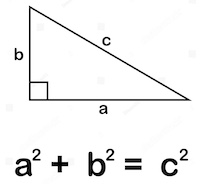
Consider a right triangle with side lengths of 3 units, 4 units, and an unknown hypotenuse. We can use the Pythagorean Theorem to find the length of the hypotenuse.
a = 3
b = 4
c² = a² + b²
c² = 3² + 4²
c²= 9 + 16
c² = 25
\(c = (\sqrt{25})\)
c=5
The square root of 25 is 5, so the length of the hypotenuse is 5 units.
Let’s Review!
- The coordinate plane is a two-dimensional number line that is used to display ordered pairs. Two-dimensional shapes can be drawn on the plane, and the length of the objects can be determined based on the given coordinates.
- The area of a two-dimensional object is the amount of space inside the shape. There are area formulas to use to calculate the area of various shapes.
- For a three-dimensional object, the surface area is the sum of the area of the faces and the volume is the amount of space inside the object. Cubes and right rectangular prisms are common three-dimensional solids.
Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
