Basic Multiplication and Division
TEAS Test – Basic Multiplication and Division
This lesson describes the TEAS test math concept of multiplying and dividing numbers and introduces the order of operations, which governs how to evaluate expressions containing multiple arithmetic operations.
TEAS Test Math – Multiplication
Addition can be tedious if it involves multiple instances of the same numbers. For example, evaluating 29 + 29 is easy, but evaluating 29 + 29 + 29 + 29 + 29 is laborious. Note that this example contains five instances—or multiples—of 29. Multiplication replaces the repeated addition of the same number with a single, more concise operation. Using the multiplication (or times) symbol (×), the expression is
29 + 29 + 29 + 29 + 29 = 5 × 29
The expression contains 5 multiples of 29. These numbers are the factors of multiplication. The result is called the product. In this case, addition shows that the product is 145. As with the other arithmetic operations, multiplication is easy for small numbers. Below is the multiplication table for whole numbers up to 12.
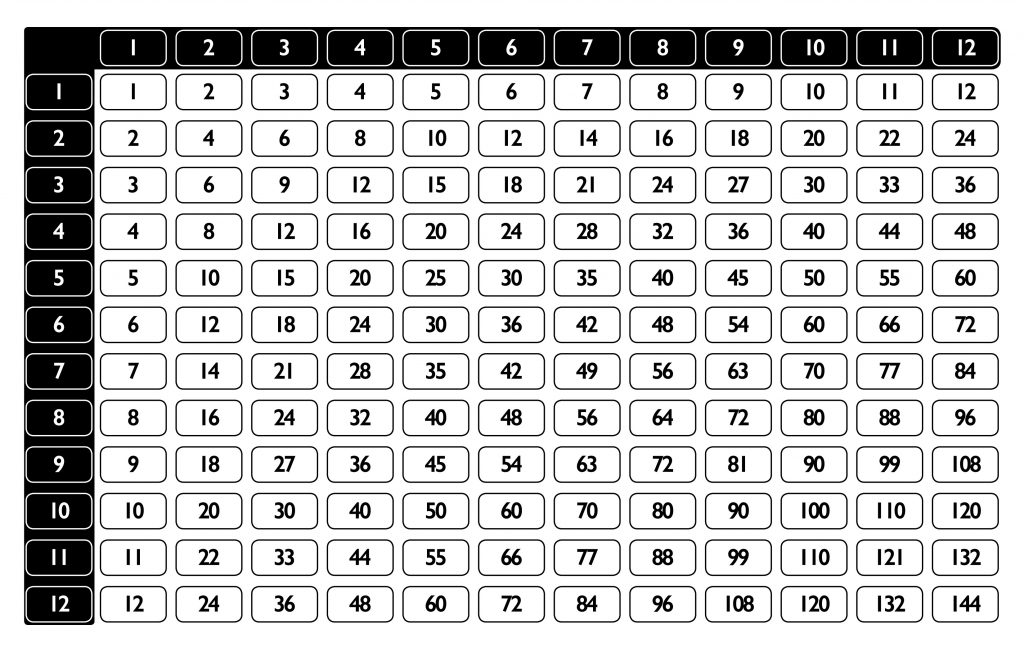
When dealing with large numbers, the multiplication algorithm is more practical than memorization. The ability to quickly recall the products in the multiplication table is nevertheless crucial to using this algorithm.
STEP BY STEP

Step 1. Stack the two factors, vertically aligning the digits in each place.
Step 2. Draw a multiplication symbol (×) to the left of the bottom number and draw a horizontal line below the stack.
Step 3. Begin with the ones digit in the lower factor. Multiply it with the ones digit from the top factor.
Step 4. If the product from Step 3 is less than 10, write it in the same column below the horizontal line. Otherwise, write the first (ones) digit below the line and carry the second (tens) digit to the top of the next column.
Step 5. Perform Step 4 for each digit in the top factor, adding any carry digit to the result. If an extra carry digit appears at the end, write it as the leftmost digit in the product.
Step 6. Going right to left, repeat Steps 3–4 for the other places in the bottom factor, starting a new line in each case.
Step 7. Add the numbers below the line to get the product.

KEY POINT
As with addition, the order of numbers in a multiplication expression is irrelevant to the product. For example, 6 × 9 = 9 × 6.
TEAS Test Math – Multiplication Review
TEAS Test Math – Division
Division is the inverse of multiplication, like subtraction is the inverse of addition. Whereas multiplication asks how many individuals are in 8 groups of 9 (8 × 9 = 72), for example, division asks how many groups of 8 (or 9) are in 72. Division expressions use either the / or ÷ symbol. Therefore, 72 ÷ 9 means: How many groups of 9 are in 72, or how many times does 9 go into 72? Thinking about the meaning of multiplication shows that 72 ÷ 9 = 8 and 72 ÷ 8 = 9. In the expression 72 ÷ 8 = 9, 72 is the dividend, 8 is the divisor, and 9 is the quotient.
When the dividend is unevenly divisible by the divisor (e.g., 5 ÷ 2), calculating the quotient with a remainder can be convenient. The quotient in this case is the maximum number of times the divisor goes into the dividend plus how much of the dividend is left over. To express the remainder, use an R. For example, the quotient of 5 ÷ 2 is 2R1 because 2 goes into 5 twice with 1 left over.
Knowing the multiplication table allows quick evaluation of simple whole-number division. For larger numbers, the division algorithm enables evaluation by hand.
Unlike multiplication—but like subtraction—the order of the numbers in a division expression is important. Generally, changing the order changes the quotient.
STEP BY STEP

Step 1. Write the divisor and then the dividend on a single line.
Step 2. Draw a vertical line between them, connecting to a horizontal line over the dividend.
Step 3. If the divisor is smaller than the leftmost digit of the dividend, perform the remainder division and write the quotient (without the remainder) above that digit. If the divisor is larger than the leftmost digit, use the first two digits (or however many are necessary) until the number is greater than the divisor. Write the quotient over the rightmost digit in that number.
Step 4. Multiply the quotient digit by the divisor and write it under the dividend, vertically aligning the ones digit of the product with the quotient digit.
Step 5. Subtract the product from the digits above it.
Step 6. Bring down the next digit from the quotient.
Step 7. Perform Steps 3–6, using the most recent difference as the quotient.
Step 8. Write the remainder next to the quotient.

KEY POINT
Division by 0 is undefined. If it appears in an expression, something is wrong.
TEAS Test Math – Division Review
Signed Multiplication and Division
Multiplying and dividing signed numbers is simpler than adding and subtracting them because it only requires remembering two simple rules. First, if the two numbers have the same sign, their product or quotient is positive. Second, if they have different signs, their product or quotient is negative.
As a result, negative numbers can be multiplied or divided as if they are positive. Just keep track of the sign separately for the product or quotient. Note that negative numbers are sometimes written in parentheses to avoid the appearance of subtraction.
For Example:
5 × (–3) = –15
(–8) × (–8) = 64
(–12) ÷ 3 = –4
(–100) ÷ (–25) = 4
TEAS Math – Signed Multiplication and Division Review
TEAS Test Math – Orders of Operations
By default, math expressions work like most Western languages: they should be read and evaluated from left to right. However, some operations take precedence over others, which can change this default evaluation. Following this order of operations is critical. The mnemonic PEMDAS (Please Excuse My Dear Aunt Sally) helps in remembering how to evaluate an expression with multiple operations. Knowing the order operations is a common TEAS test math question so you’ll need to be very familiar with PEMDAS.
STEP BY STEP

| P | Evaluate operations in parentheses (or braces/brackets). If the expression has parentheses within parentheses, begin with the innermost ones. |
| E | Evaluate exponential operations. (For expressions without exponents, ignore this step.) |
| MD | Perform all multiplication and division operations, going through the expression from left to right. |
| AS | Perform all addition and subtraction operations, going through the expression from left to right. |
Because the order of numbers in multiplication and addition does not affect the result, the PEMDAS procedure only requires going from left to right when dividing or subtracting. At those points, going in the correct direction is critical to getting the right answer.
Calculators that can handle a series of numbers at once automatically evaluate an expression according to the order of operations. When available, calculators are a good way to check the results.

BE CAREFUL!
When evaluating an expression like 4 – 3 + 2 × 5, remember to go from left to right when adding and subtracting or when multiplying and dividing. The first step in this case (MD) yields 4 – 3 + 10. Avoid the temptation to add first in the next step; instead, go from left to right. The result is 1 + 10 = 11, not 4 – 13 = –9.
Try this TEAS math practice question
TEAS Test Math – Order of Operations Review
Working with Exponents
When following the order of operations, the second operation to evaluate within an expression are the exponents. Exponents imply an expression of repeated multiplication, otherwise known as a power. The exponent is a super scripted number for the number of times the base is multiplied. For example, \(6^2\) is the same as 6 times 6, or 36.
It is important to understand that any base to a power of 0 will equal 1. Otherwise written as a rule \(n^0 = 1\). For example, \(3^0 = 1\).
When exponents are written as negative values, these expressions are considered fractions or decimals. The value will be one portion of the base number and the exponent as a positive number. For example, \(2^{–2} =\frac{1}{2^2}=\frac{1}{4}\).
Negative exponents are commonly used to represent small decimal numbers with a base of 10. For example, the expression \(10^{–3}\) is equivalent to \(\frac{1}{1000}\) or 0.001
These rules are summarized in the chart below.
| Property | Definition | Examples |
| Zero Exponent Rule | \(a^0=1\) | \(64^0=1\), \(y^0=1\) |
| Negative Exponent Rule | \(a^{-m}=\frac{1}{a^m}\) | \(3^{-3}=\frac{1}{3^3}=\frac{1}{27}\), \(\frac{1}{x^{-3}}=x^3\) |
Try this exponents practice question
This material will be further covered in a later section. Please refer to our video in “TEAS Math Powers & Exponents” for further instruction.
Let’s Review!
- The multiplication table is important to memorize for both multiplying and dividing small whole numbers (up to about 12).
- Multiplication and division of large numbers by hand typically requires the multiplication and division algorithms.
- Multiplying and dividing signed numbers follows two simple rules: If the numbers have the same sign, the product or quotient is positive. If they have different signs, the product or quotient is negative.
- When evaluating expressions with several operations, carefully follow the order of operations; PEMDAS is a helpful mnemonic.
In the next lesson we move to the TEAS math topic of decimals and fractions.
You May Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
