Scientific Measurement
TEAS Science Prep – Scientific Measurement
In the previous lesson you learned the TEAS science prep lesson for the scientific method and designing an experiment. Now this TEAS science prep lesson about the scientific reasoning reviews the scientific tools used in experiments to measure pressure, mass, length, time, and liquids. In addition, it reviews scientific measures and scientific notation.
TEAS Science Prep – Scientific Tools
Researchers use a wide variety of tools to collect data. The most common types of measuring tools are outlined below:
- Barometer: Used to determine the air pressure in a space.
- Clock or stopwatch: Used to record time.
- Graduated cylinder: Used to measure the volume of liquid.
- Ruler: Used to measure the length of an object.
- Glass pipette: Used to measure and transfer precise volumes of liquid. They are particularly useful for small volumes where accuracy is crucial.
- Glass micropipettes: used to measure very small volumes of liquids typically in the microliter (µL) to nanoliter (nL) range. They offer high precision and accuracy for tiny volumes.
- Thermometer: Used to measure temperature. Measurement values may be expressed in degrees Celsius or Fahrenheit.
- Triple beam balance: Used to measure an object’s mass or determine the unit of mass. Electronic balances are used to measure very small masses.
When measuring liquids, one would not utilize beakers or flasks in a laboratory setting. This is because these tools are primarily used for mixing, heating, and holding liquids. They have graduations (measurement markings), but these are often not very precise. The wide openings and larger surface areas make it difficult to measure exact volumes accurately.
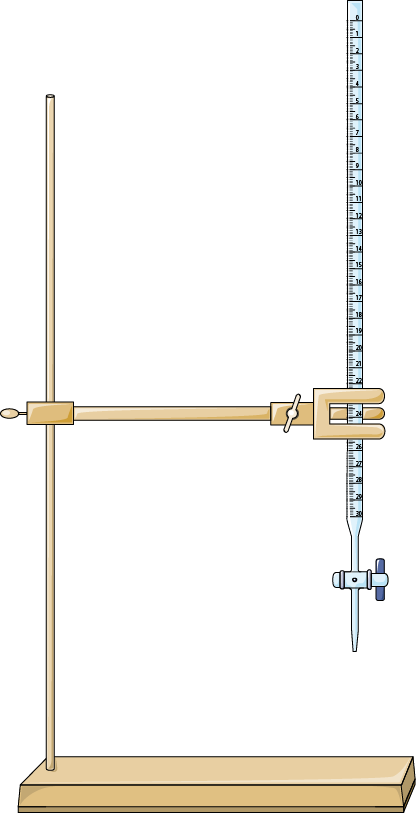
Burette [Source]
To accurately measure liquids, use the following tools:
- Graduated cylinders: These are specifically designed for measuring the volume of liquids. They have a narrow shape and more precise graduations, allowing for more accurate measurements.
- Burettes are used in titrations. They provide precise volume measurements and control, allowing for liquid dispensing in small, accurate increments.
- Pipettes: They accurately measure and transfer small volumes of liquid. Micropipettes can measure volumes as small as microliters with high precision.
When measuring liquids in a graduated cylinder, it’s crucial to account for the meniscus, which is the curve seen at the surface of a liquid due to the adhesion of the liquid to the container walls and the cohesion of the liquid molecules to each other.
Concave Meniscus
A concave meniscus curves upward at the edges and downward in the middle, typical of liquids like water that wet the container walls. When measuring such liquids, the volume should be read at the lowest point of the curve, as this point represents the true level of the liquid.
This occurs because adhesive forces pull the liquid up the sides of the container. For example, when measuring water in a graduated cylinder, ensure you read the volume at the bottom of the meniscus.
Convex Meniscus
A convex meniscus curves downward at the edges and upward in the middle, commonly seen in liquids like mercury and other non-wetting substances. When measuring such liquids, the volume should be read at the highest point of the curve. This is because the cohesive forces pull the liquid up in the middle, making the highest point the true level of the liquid.
For example, when measuring mercury in a graduated cylinder, read the volume at the top of the meniscus.
TEAS Science Prep – Scientific Measurements
Measured values are often associated with scientific units. Typically, the metric system is preferred when reporting scientific results. This is because nearly all countries use the metric system. Additionally, there is a single base unit of measurement for each type of measured quantity. For example, the base unit for length cannot be the same as the base unit for mass. The following base units are used:
| Unit of Measurement | Base Unit Name | Abbreviation |
| Length | Meter | m |
| Mass | Gram | g |
| Volume | Liter | L |
Understanding which units of measurement to use in different contexts is crucial for accuracy in scientific, health science, and everyday applications.
Grams (g)
Grams are ideal for measuring the mass of light objects. If the object can be easily held in your hand and does not feel heavy, it is likely measured in grams.
Examples:
- Ingredients in a recipe (e.g., flour, sugar)
- Medication dosages
Kilograms (kg)
Kilograms are used to measure the mass of heavier objects. This unit is suitable for items that are substantial in weight. If lifting the object requires effort, you will likely use kilograms as your unit.
Examples:
- Body weight of humans
- Medical devices and equipment such as weighted blankets or therapy balls
Meters (m)
Meters are used to measure longer distances or lengths of large objects and spaces.
Examples:
- Length of football field
- Height of a building
- Length of a room
Centimeters (cm)
Centimeters are ideal for measuring smaller lengths and heights where precision is necessary.
Examples:
- Height of a plant
- Dimensions of a book
- Waist size in clothing
- Length of wound or scar
Another benefit of the metric system is that units are expressed in multiples of 10. This allows a researcher to express reported values that may be very large or small. This expression is facilitated by using the following metric prefixes, which are added to the base unit name:
| Prefix | Abbreviation | Value | Description |
|---|---|---|---|
| kilo | k | 1,000 | thousand |
| hecto | h | 100 | hundred |
| deka | da | 10 | ten |
| BASE | N/A | 1 | one |
| deci | d | 0.1 | tenth |
| centi | c | 0.01 | hundredeth |
| milli | m | 0.001 | thousandth |
Conversions are crucial for several reasons, including ensuring measurement consistency, standardization, and data integrity. They contribute to precision and accuracy, providing exact measurements that help avoid mistakes. In the medical field, conversions are vital for practical applications such as precision and safety in medication dosages, accurate patient measurements for BMI calculations and medical records, and nutritional planning. Additionally, they play a significant role in research and development by ensuring experimental consistency and enabling data comparison.
Try this Science TEAS 7 practice test question
TEAS Science Prep – Scientific Notation
Scientists often work with very large and very small numbers. For example, the radius of Earth’s orbit around the sun is very large: 15,000,000,000,000 centimeters. On the other extreme, the radius of a hydrogen atom is very small: 0.00000000529 centimeters. To make these numbers more manageable, scientists write them using scientific notation. Scientific notation is a way to represent numbers and contains three components, which are shown in the diagram below.
Understanding how these components relate to one another makes it possible to convert between standard notation and scientific notation. The coefficient is a number that has a value of at least 1 but less than 10 and includes all significant digits in the given value. Another way to think about this is that there should always be one non-zero digit before the decimal point.
In scientific notation, the base is always 10.

The exponent indicates the number of places the decimal point needs to move. Notice that when the exponent is positive, the decimal place moves to the right; this is how larger numbers are represented. When the exponent is negative, the decimal place moves to the left; this is how smaller numbers are represented. When the decimal must move beyond the digits that are in the measurement, the “empty” spaces are filled in with zeros.
Let’s Review
- Different devices are used to measure objects in an experimental study.
- The metric system is usually used when expressing the units of measured values.
In the next TEAS science prep lesson you’ll learn about macromolecules.
You May Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
