Friction and Types of Motion
This lesson discusses different types of motion. Then, it examines uniform circular (rotational) motion and centripetal acceleration. It also introduces the concept of friction and its effect on motion in real-world situations.
Types of Motion
According to Newton’s first law of motion, an object moving with a given velocity (even if it is zero) will maintain that velocity indefinitely unless some net force acts on it. Absent any net force, the object will move in one direction along a line (assuming a nonzero speed). In this case, the object exhibits linear motion because its movement is in only one spatial dimension. If a force acts on the object and that force is parallel with the dimension in which the object is moving, the acceleration will be parallel or antiparallel (exactly opposite in direction) to the velocity. Thus, even though the object will speed up or slow down, its motion will remain linear.
If a force acts on an object in a direction that is not parallel to the object’s velocity, the object no longer moves along a line; it exhibits nonlinear motion. Passengers riding in a car, for example, can tell the difference between linear and nonlinear motion by the direction of the force they feel as they ride. If the car speeds up or slows down linearly, they will feel only a backward force (positive acceleration) or a forward force (negative acceleration, or deceleration). If it turns (nonlinear motion), the passengers will feel a force toward either side as the car turns in some direction.
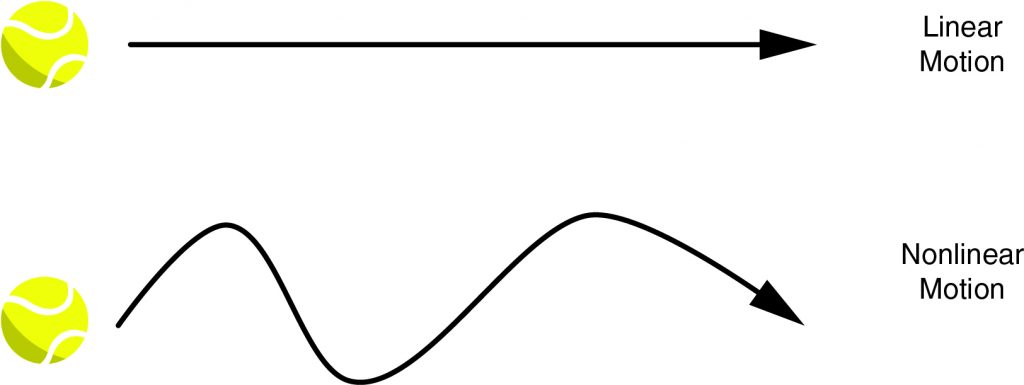
In general, mathematically analyzing nonlinear motion requires vector calculus. However, in certain cases, nonlinear motion can be described using only algebra. One case is rotational motion, which involves objects spinning on an axis or moving in a circle around some central point. Because rotational motion involves circular geometry, it is also commonly called circular motion.
Uniform Circular Motion
An object that rotates about an axis or revolves circularly around some point exhibits rotational motion (or circular motion). A simple case that provides a foundation for more-complex analysis is an object moving in a circle around some point outside its surface. For example, consider a ball tied to the end of a stick by a string. If someone holds the stick and causes the ball to move a circle, the ball will always be a fixed distance from the end of the stick—that distance is the length of the string. If such an object moves with a constant speed, its movement is called uniform circular motion.
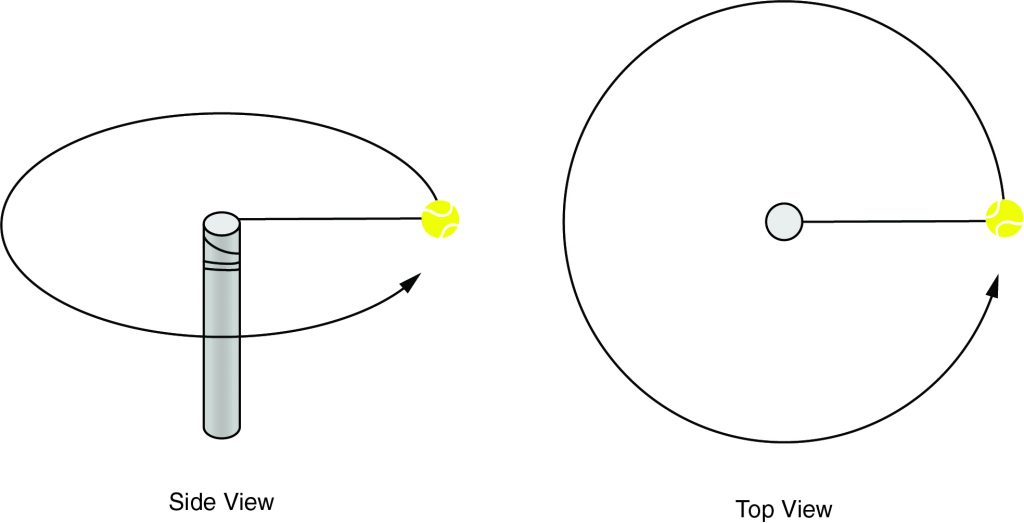
The speed of an object in uniform circular motion is, like in linear motion, a distance divided by the time required to traverse that distance. A simple expression is the circumference of the circle divided by the time the object takes to go around one full time. Given a radius r and a time T to go around the circle, the speed v is \(v=\frac{2pi r}{T}\)
This time T is also called the object’s period, and its inverse \((frac{1}{T})\) is the frequency, often expressed as f. The frequency measures how often the object completes a revolution around the circle, and its unit (when T is in seconds) is hertz (Hz). Another useful quantity is the angular frequency, 2πf, which is often expressed as ω and may also use hertz. Employing this definition, the velocity is ωr. Therefore, the velocity v is also equal to 2πfr.

DID YOU KNOW!
In the case of a ball on a string, if at any point the string is cut, removing the force acting on the ball, the ball will immediately begin moving linearly at the same speed with which it was moving circularly. Its direction will be tangential to the circle—that is, the direction of its velocity at the moment the string is cut.
Centripetal Acceleration
Although the speed of an object in uniform circular motion is constant, its velocity is always changing: it is at all points tangent to the circular path. By Newton’s first law of motion, therefore, the object is experiencing acceleration and thus a force. This acceleration—called centripetal acceleration—always points toward the center of the circle. A simple example is a planet, such as Earth, orbiting a star. The star exerts a gravitational force that pulls the planet toward the star, and the planet moves (ideally) in a circle around the star. The derivation of centripetal acceleration \((a_c)\) is complicated, but the formula is simple given a speed v and a radius r: \(a_c=\frac{v^2}{r}\).

TEST TIP
If you are unsure whether you correctly remember a formula, such as centripetal acceleration, you can increase your confidence by checking the units. For instance, using metric units, acceleration is in units of \(m/s^2\). Velocity squared yields units of \(m^2/s^2\), and the radius is in units of m. Dividing the squared velocity units by the radius units yields \(m/s^2\), which is the same as for acceleration. This check is not sufficient to prove the formula is correct, but it can identify an erroneous formula.
By Newton’s second law of motion, the centripetal force Fc on an object of mass m is therefore \(F_c=ma_c=\frac{mv^2}{r}\).
Centrifugal force is a “ghost” force. For example, a passenger in a car that turns right feels a leftward force. But by Newton’s first law of motion, the passenger’s body tries to keep moving straight when the car turns right, causing the car to push the passenger to the right. The feeling, however, is of another force pushing the passenger leftward into the car rather than the car pushing the passenger rightward toward the center of rotational motion. The centrifugal force is therefore equal in magnitude but opposite in direction to the centripetal force.
Friction
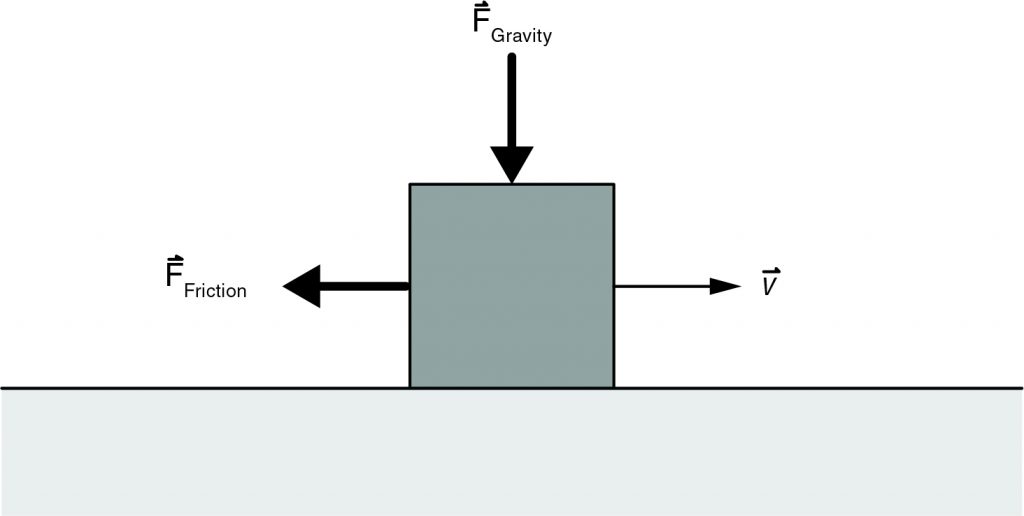
Newton’s first law of motion seems to break down in everyday life: rolling cars come to a stop, falling objects stop accelerating at a certain speed despite the force of gravity, and so on. The cause of the apparent breakdown is another force that resists the motion of objects: friction. For example, a plane that turns off its engines loses horizontal speed because of air resistance, which is a type of friction. A heavy piece of furniture is often difficult to slide across a floor because it experiences friction wherever it touches the floor. Friction can also act on non-moving objects. For instance, it can prevent an object from sliding down an incline despite the force of gravity.
Because friction is a force, it causes acceleration. For moving objects, the friction force generally has a direction opposite that of the velocity. When an object decelerates because of friction, byproducts of this deceleration can be a motion of something else (such as waves or eddies when the object is moving in water) or heat. Heat is another type of motion that involves the movement of the atoms and molecules that constitute matter. For example, people with cold hands may rub them together briskly to warm them. For stationary objects, the force of friction is opposite to what would otherwise be a net force, such as gravity.
A common example of friction is an object sliding on a surface. The force due to friction is proportional to the object’s mass because the mass determines the object’s weight (which is the force it experiences from gravity). The weight of an object causes it to “push” against the surface, and when the object slides, that vertical push creates the resistance to horizontal motion (that is, friction) because of surface imperfections and irregularities.

KEEP IN MIND
Calculating the friction force can be difficult because it involves many factors, such as the roughness of surfaces (in the case of sliding objects) and the fluid characteristics of air (in the case of air resistance). For this reason, problems often assume friction is negligible—an assumption that often still allows a good approximation of the solution.
Let’s Review!
- Linear motion is movement along a line; the velocity and acceleration may vary, but they are always parallel to the line.
- Nonlinear motion is movement that is not confined to a line; the velocity and acceleration can be any quantity.
- Rotational (circular) motion is movement around an axis or along a circular path.
- The period (T) of an object in a uniform circular motion is the time it takes to travel once around the circle. The inverse of the period is the frequency (f), and the angular frequency (ω) is 2πf.
- Centripetal acceleration \(a_c\) is the acceleration an object experiences when in a uniform circular motion. It is equal to \(\frac{v^2}{r}\) where v is the object’s velocity and r is the radius of the circle of motion.
- The centripetal force on an object in uniform circular motion is the object’s mass times its centripetal acceleration.
- Centrifugal force is a “ghost force” in which an object undergoing centripetal acceleration “feels” like it is being pushed away from the center of rotation.
- Friction is resistance to motion. It is a force that is generally directed opposite to a moving object’s velocity.
- Friction causes heat and/or motion of surrounding materials as a byproduct of its force on a moving object.
- Friction can prevent motion by acting opposite to other forces, such as gravity.
You May Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
