Waves and Sound
This lesson reviews a simple model of the atom and its role in the materials of everyday life. It then discusses waves in general and mechanical and electromagnetic waves in particular and applies these principles to optics.
Matter and Atomic Structure
The materials that are common to human experience (through sight, touch, and the other senses) have an invisible, microscopic structure that experimenters can probe using scientific instruments. The fundamental unit of this structure is the atom, which comprises a central, heavy nucleus (plural nuclei) surrounded (“orbited”) by lighter electrons. The nucleus is composed of protons, which carry a positive electric charge, and neutrons, which carry no electric charge (they are electrically neutral). Together, the protons and neutrons are sometimes called nucleons. Electrons carry a negative electric charge. Below is a simple representation of the structure of an atom.
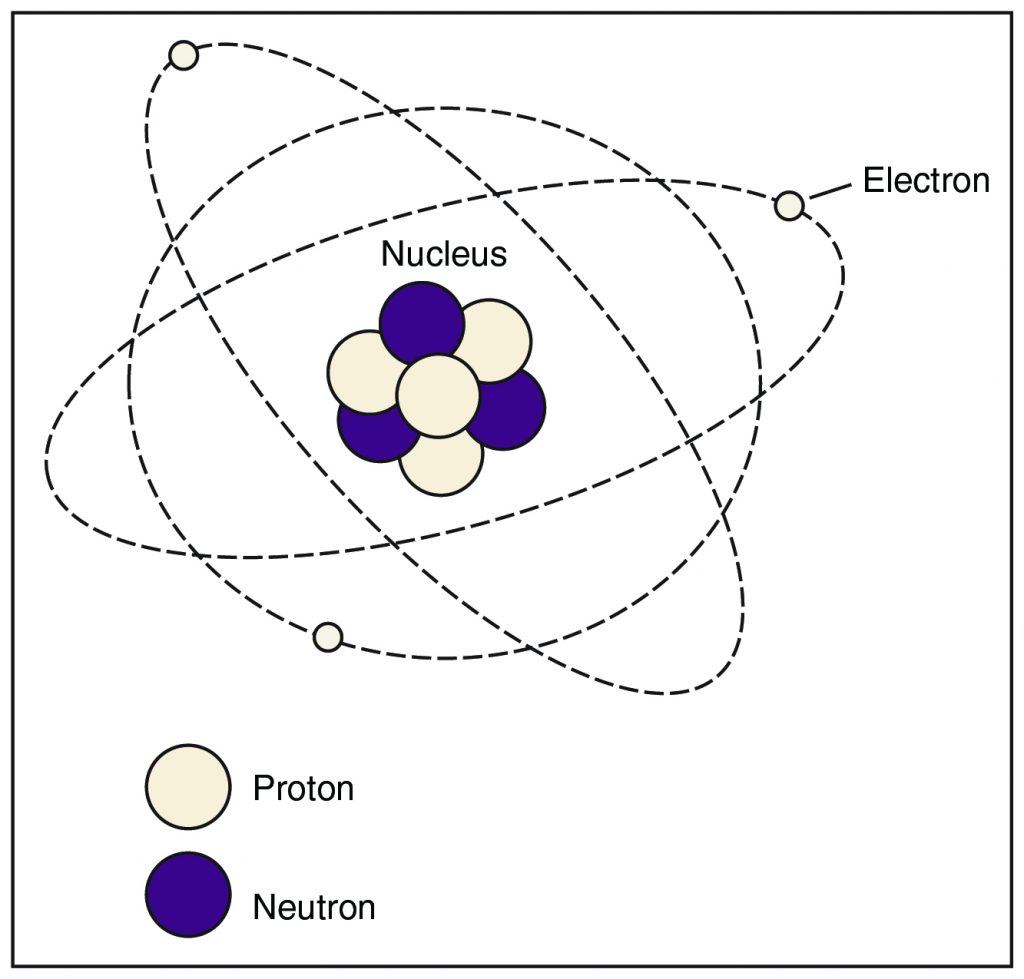
Electric charge (or just “charge”) is a property of matter that relates to attraction or repulsion through the electric force. Charge comes in two known varieties; although scientists use positive and negative to describe charge, these terms are just conventions that have some mathematical utility. They do not describe a fundamental “signed” property of charge. The main qualitative rule is that like charges repel and unlike charges attract.
The electric force holds the atom together through the attraction of the negatively charged electrons to the positively charged nucleus. When an atom has the same number of electrons as protons, it is electrically neutral because the amount of charge on an electron is the same as that on a proton, but they are unlike, causing electrical attraction. The result is the simplistic model of an atom that shows electrons orbiting the nucleus like planets orbit the sun.
The number of protons in a nucleus determines the element that the atom represents: hydrogen (1 proton), helium (2), carbon (6), oxygen (8), iron (26), and so on. The number of neutrons in a nucleus can vary. Instances of an element with different neutron counts are called isotopes of that element. As a rule, isotopes of common elements have about as many neutrons as protons.
If the number of electrons in an atom differs from the number of protons, that atom has a net electric charge: positive if it has more protons than electrons, and negative if it has more electrons than protons. An atom with a net electric charge is called an ion.
Although not all matter is composed of atoms—physicists claim to have discovered a variety of particles that can exist apart from atoms—an understanding of atomic structure informs numerous fields, including chemistry and semiconductor physics. Moreover, the nucleons of an atom appear to have a deeper internal structure, a topic that researchers are exploring.
Properties of Waves
A universally recognizable example of waves is in water—whether in the ocean, a pool, or a small container. It is possible to visualize many aspects of invisible and conceptual, or mathematical, waves by observing how waves act in water. For example, the highest part of an ocean wave is the crest (or peak), the lowest part is the trough, and half the distance between these two points is the amplitude. (The full distance between the crest and trough is called the peak-to-peak amplitude.) The distance between successive peaks or successive troughs is called the wavelength. These parameters describe the spatial (space-related) characteristics of the wave. But waves also generally have temporal (time-related) characteristics. For example, given some fixed point in space, the time between the arrival of successive waves is the period, and its reciprocal is the frequency—often expressed in hertz (Hz), or inverse seconds \((s^{–1})\).
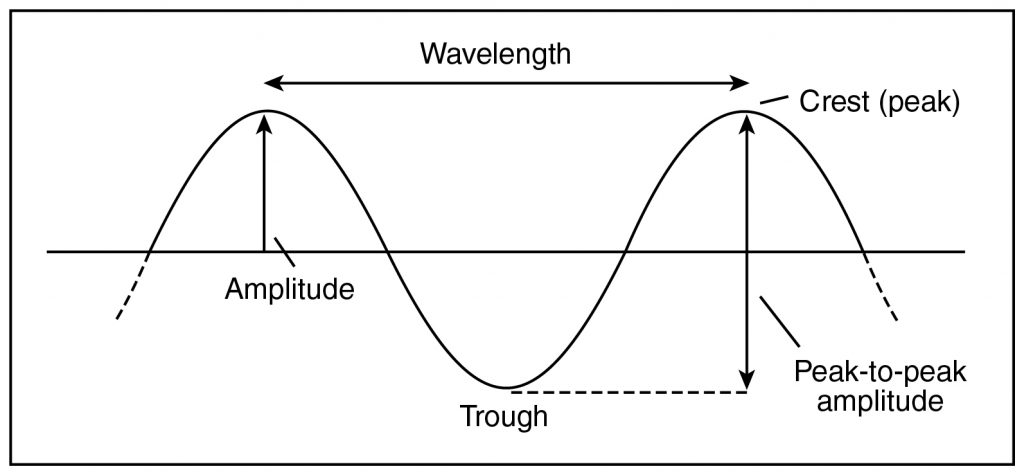
The wavelength (λ), frequency (f), and wave speed (v) are related by the equation v = λf.
Although these spatial and temporal properties are the most intuitive, waves can have other, less intuitive properties. For instance, if a light source increases and decreases in intensity over time, its intensity can be described as a wave whose frequency is temporal and whose amplitude is intensity (rather than height). Mechanical (e.g., sound and water) and electromagnetic (e.g., visible light and radio) waves are additional examples.
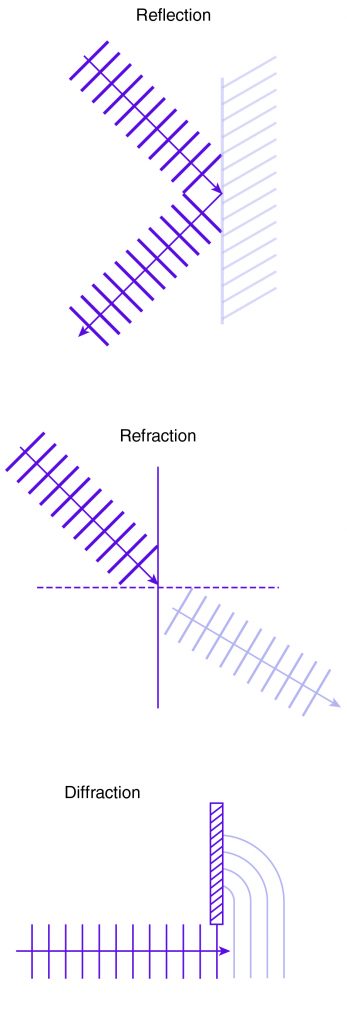
Water waves also demonstrate some of the general behaviors of waves. When they strike a wall or other fairly stationary object, for example, the result is reflection: some or all of the wave “bounces” off the object. Waves that pass through a medium with changing material properties may bend, a phenomenon called refraction. The changing depth of the ocean floor, for instance, causes ocean waves to bend and usually arrive perpendicular to shore, regardless of their original direction. Another behavior of waves is diffraction: waves traveling in a certain direction can “turn” around sharp edges.
Mechanical Waves
Waves that propagate in matter—for example, water waves—are called mechanical waves. They can involve variation in height, as in water waves, or variation in pressure, as in acoustic/sound waves. Earthquakes involve mechanical waves similar to sound waves: these seismic waves cause the ground to shake as they travel from the source of the quake.
In the case of sound, what the ear detects as pitch is essentially the frequency of the wave, and the volume is essentially the amplitude. Characteristics of the wave, including its speed, depend on the properties of the medium (or substance/material) that carries it. In the case of sound, for example, the wave speed depends on the density of the medium—how many atoms are packed into a unit volume—and the compressibility of the medium—how much the medium can be compacted given a certain force or pressure. The denser and less compressible a material, the faster sound waves will travel through it. Because water is denser and less compressible than air, for instance, sound travels faster in the former than in the latter. Similarly, waves in a rope will travel faster if the rope is taut than if it is loose.
Depending on the type of mechanical wave and the medium through which it travels, the wave speed may be apparent to the human senses. For example, at a sufficiently large distance from the observer, an event such as a hammer strike or gunfire is visible before it is audible. This delay occurs because light travels much faster than sound. Therefore, distant events are often seen before they are heard.
Mechanical waves exhibit the same phenomena as other waves, such as reflection, refraction, and diffraction.
Electromagnetic (Light) Waves
Electromagnetic waves exhibit the same behavior as other waves, but unlike mechanical waves, they require no medium to propagate. (That is, they can propagate in a vacuum.) Electromagnetic waves result from the movement—specifically, the acceleration—of a charge. Examples include visible light, radio waves, X-rays, microwaves, and infrared radiation.
As their name implies, electromagnetic waves involve variation in the electric field and the magnetic field around the source charge(s). These fields mutually oscillate in a manner similar to that of mechanical waves, although the oscillation is in field intensity and direction rather than, for example, wave height or material pressure.
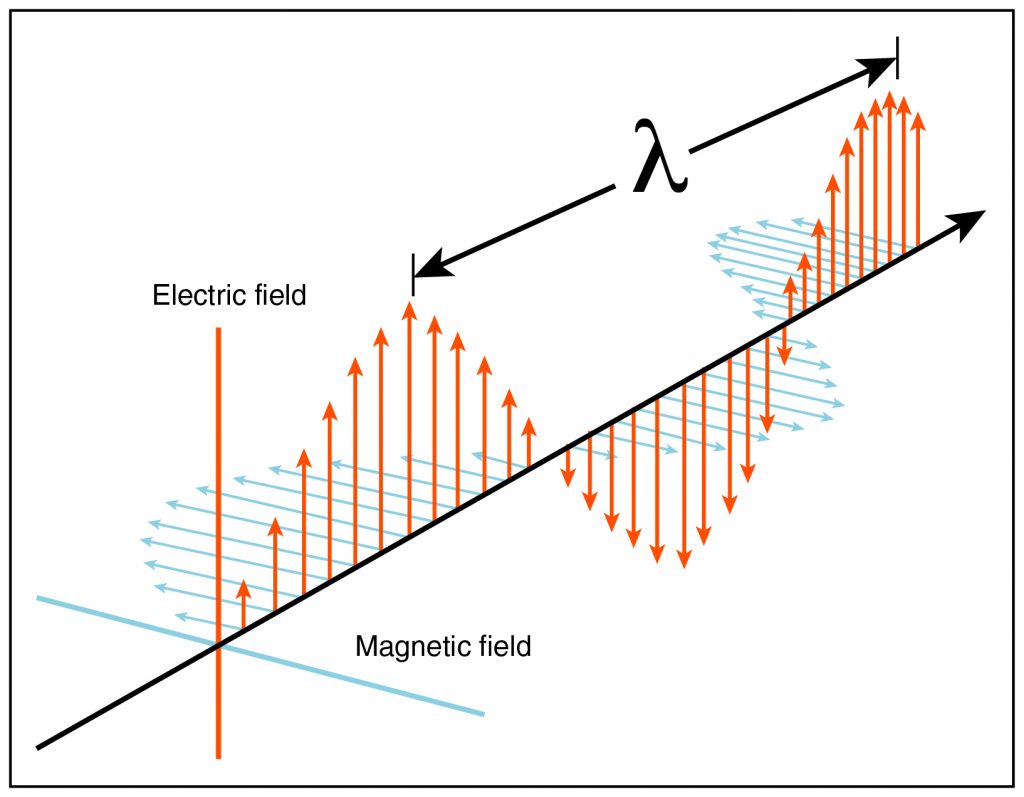
In a vacuum, the speed of an electromagnetic wave (or the speed of light, sometimes labeled c) is a constant: approximately 186,000 miles per second, which is much faster than the speed of sound in air—roughly 0.2 miles per second, or about 770 miles per hour. When traveling in a material, the speed of an electromagnetic wave decreases by a factor of 1/n, where n is the material’s refractive index (or index of refraction). Therefore, the speed of light v in a material of refractive index n is v = c/n. The refractive index depends on the electrical and magnetic properties of the material.

CONNECTIONS
Electromagnetic wave behaviors include reflection (e.g., looking in a mirror), refraction (e.g., looking through a prism and seeing objects at off angles), and diffraction (e.g., shifting multicolored patterns on a compact disc).
Optics
In situations where the dimensions of a problem are much larger than the wavelength of the electromagnetic waves, those waves can often be accurately approximated as rays: directed line segments that represent the waves. Some simple rules enable analysis of electromagnetic-wave behavior in media that involve mirrors and in materials with different refractive indices. This model is a straightforward, often effective way to study optics, which is the subset of physics that examines the behavior of light.
DID YOU KNOW?

A laser acts as like nearly ideal ray because it maintains a very narrow beam over long distances. When used with caution (specifically, eye protection), low-power lasers are excellent for clearly seeing the principles of optics in action.
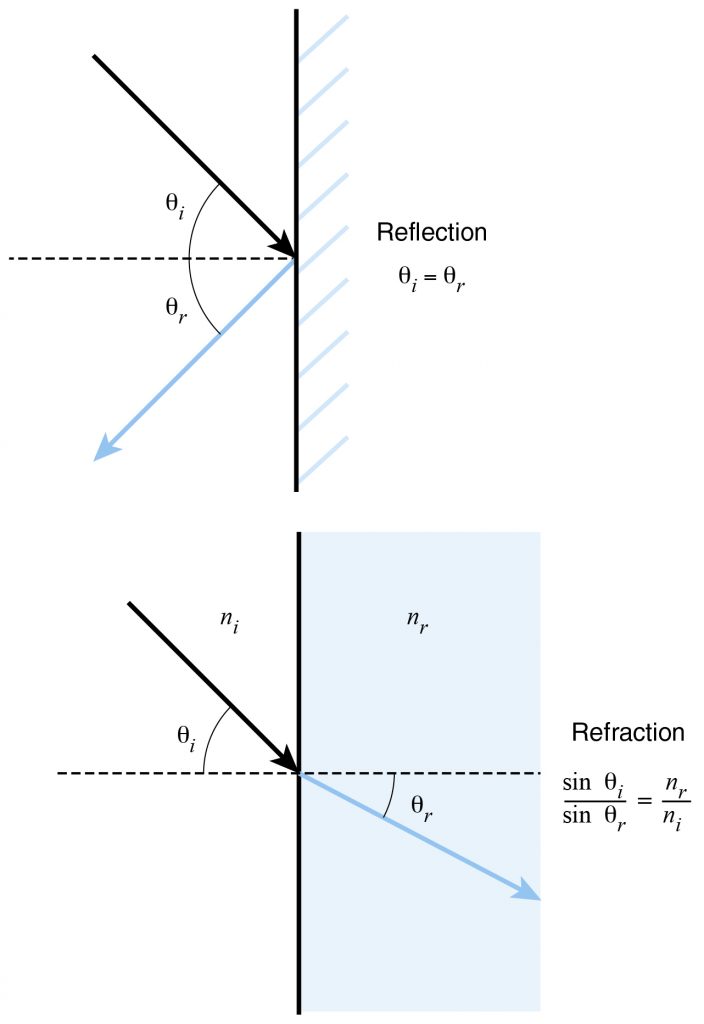
Many problems in optics can be analyzed using two simple rules. First, for a reflective surface (mirror), the angle of incidence of a ray is equal to the angle of reflection. Both angles are measured from a line perpendicular—or normal—to the surface and passing through the point at which the ray meets that surface. In the case of reflection, the angles can also be measured relative to a line parallel to the surface at that point. Second, for a ray passing from a material with one refractive index to a material with a different refractive index, the formula below relates the angle of incidence \((θ_i)\) to the angle of refraction \((θ_r)\), where \(n_i\) is the refractive index of the material from which the ray originates and \(n_r\) is the refractive index of the material into which the ray transmits. This relationship is called Snell’s law and is responsible for the magnification of objects using lenses.
\(\frac{sin theta_i}{sin theta_r}=\frac{n_r}{n_i}\)
Let’s Review!
- The matter that appears in everyday life is largely composed of atoms; each atom has a central nucleus made of positively charged protons and uncharged neutrons that is surrounded by “orbiting” negatively charged electrons.
- The elements are each a type of atom with a different number of protons in its nucleus. A given element with a given number of neutrons is an isotope.
- The electric force binds the electrons to the nucleus of an atom.
- Waves occur throughout nature in different forms, but they have common properties and behaviors.
- A wave is defined by its amplitude, frequency, and wavelength. The wave speed is equal to the product of the frequency and the wavelength (v = λf).
- Common wave behaviors include reflection (when the wave “bounces” off an object), refraction (when it bends in a medium), and diffraction (when it turns around an edge).
- Mechanical waves are waves in a material—solid, liquid, or gas. Examples include sound waves, seismic waves, and ocean waves.
- The speed of a mechanical wave depends on the compressibility and density of a material. As these values increase, so does the wave speed.
- Electromagnetic waves are a back-and-forth oscillation of the electric and magnetic fields owing to acceleration of a charge. They can propagate without a medium (that is, in a vacuum).
- The speed of an electromagnetic wave in a material is equal to the speed of light in a vacuum (c) divided by the refractive index of that material.
- In optics, the angle of incidence of a light ray is equal to the angle of reflection.
- Refraction of a ray is described by Snell’s law:
- \(\frac{sin theta_i}{sin theta_r}=\frac{n_r}{n_i}\)
- Where \(θ_i\) is the angle of incidence, \(θ_r\) is the angle of refraction, \(n_i\) is the refractive index in the material from which the ray is traveling, and \(n_r\) is the refractive index in the material to which the ray is traveling.
Subscribe to the online course to gain access to the full lesson content.
If your not ready for a subscription yet, be sure to check out our free practice tests and sample lesson at this link
